- Proceedings
- Open access
- Published:
Bayesian non-negative factor analysis for reconstructing transcription factor mediated regulatory networks
Proteome Science volume 9, Article number: S9 (2011)
Abstract
Background
Transcriptional regulation by transcription factor (TF) controls the time and abundance of mRNA transcription. Due to the limitation of current proteomics technologies, large scale measurements of protein level activities of TFs is usually infeasible, making computational reconstruction of transcriptional regulatory network a difficult task.
Results
We proposed here a novel Bayesian non-negative factor model for TF mediated regulatory networks. Particularly, the non-negative TF activities and sample clustering effect are modeled as the factors from a Dirichlet process mixture of rectified Gaussian distributions, and the sparse regulatory coefficients are modeled as the loadings from a sparse distribution that constrains its sparsity using knowledge from database; meantime, a Gibbs sampling solution was developed to infer the underlying network structure and the unknown TF activities simultaneously. The developed approach has been applied to simulated system and breast cancer gene expression data. Result shows that, the proposed method was able to systematically uncover TF mediated transcriptional regulatory network structure, the regulatory coefficients, the TF protein level activities and the sample clustering effect. The regulation target prediction result is highly coordinated with the prior knowledge, and sample clustering result shows superior performance over previous molecular based clustering method.
Conclusions
The results demonstrated the validity and effectiveness of the proposed approach in reconstructing transcriptional networks mediated by TFs through simulated systems and real data.
Background
Transcription factor is one major gene regulator that governs the response of cells to changing endogenous or exogenous conditions [1]. Understanding how transcriptional regulatory networks (TRNs) induce cellular states and eventually define the phenotypes represents a major challenge facing systems biologists. So far, numerous models have been proposed to infer the transcriptional regulations by TFs including, ordinary differential equations, (probabilistic) Boolean networks, Bayesian networks, and information theory and association models, etc [2]. Ideally, the TF protein level activities are needed for exact modeling; however, due to low protein coverage and poor quantification accuracy of high throughput proteomics technologies such as protein array and liquid chromatography-mass spectrometry (LC-MS), the measurements of TF protein activities are currently hardly available. As a compromise, most of the aforementioned models conveniently yet inappropriately assume the TF’s mRNA expression as its protein activity. Given the fact that gene mRNA expression and its protein abundance are poorly correlated [3, 4], these models cannot accurately model the transcriptional cis-regulation or reveal at the best TF trans-regulation.
In contrast, works based on factor models [5–10] point to a natural and promising direction for modeling the TF mediated regulations, where the microarray gene expression is modeled as a linear combination of unknown TF activities, and the loading matrix in this model indicates the strength and the type (up- or down- regulation) of regulation. However, due to distinct features of TF regulation, conventional FA model is not readily applicable. First, due to various reasons (normal and disease, cancer grade, subtypes, etc), the samples are usually not independent with each other but show some clustering effect; while in the existing FA models, factors are typically assumed independent, which, although true in many applications, is not a realistic assumption for TF medicated regulation. Secondly, since a TF only regulates a small subset of genes, the loading matrix should be sparse. While with constructions of TF regulation databases, such as TRANSFAC [11], the knowledge of TF regulated genes becomes increasingly available, and should be included in the model so as to boost signal-to-noise and improve performance [12]. The inclusion of prior information and sparsity constraint naturally call for a Bayesian solution. As an added advantage, having this prior knowledge actually resolves the factor order ambiguity of the conventional factor analysis. Thirdly, as suggested in [13–15], the non-negative assumption on TF activities be imposed.
In a response to these requirements of modeling TF mediated regulatory networks, we propose here a novel Bayesian non-negative factor model (BNFM). Different from conventional factor analysis models, BNFM consists of a sparse loading matrix and a set of correlated non-negative factors. The sparsity of the loading matrix is constrained by a sparse prior [16] that directly reflects our existing knowledge of TF regulation. That is if a gene is known to be regulated by a TF, then the prior probability that this regulation exists is high, and otherwise, very low due to the generic sparse nature of TF regulation (A TF only regulates a small number of genes in the whole genome). Because of clustering effect on the data samples, the factors in this BNFM model are considered to be correlated and modeled by a Dirichlet process mixture (DPM) prior [17]. DPM imposes a natural non-parametric clustering effect [18] among samples of the same TF and can automatically determine the optimal number of clusters. Moreover, since the activities of TFs are non-negative, they are assumed to follow a (non-negative) rectified Gaussian distribution [19]. Due to the complex nonlinear structure of the BNFM, the estimation of the model becomes analytically infeasible and highly complicated numerically. A Gibbs sampling solution is developed to infer all the relevant unknown variables.
Method
Bayesian non-negative factor model
Let  represent the n-th microarray mRNA expression profile of G genes under a specific context. In practice, microarray data y
n
register the log2 scaled (fold change of) gene expression levels under the context of interest relative to a background often obtained as the average expression levels among a variety of contexts, such as different cell lines and tumors [20, 21]. We assume that the expression level y
n
is due to the linear combination of scaled TF absolute protein activites and modeled by the following factor model
represent the n-th microarray mRNA expression profile of G genes under a specific context. In practice, microarray data y
n
register the log2 scaled (fold change of) gene expression levels under the context of interest relative to a background often obtained as the average expression levels among a variety of contexts, such as different cell lines and tumors [20, 21]. We assume that the expression level y
n
is due to the linear combination of scaled TF absolute protein activites and modeled by the following factor model

where,
x n - the n-th sample vector of the scaled activities of L TFs of interest. Particulary, the non-negativity of x n is modeled by applying the component-wise rectification (or cut) function cut to a vector pseudo factors s n , such that the l-th element of x n is expressed as

Since clustering effects may exist among samples, the samples should be correlated. Therefore, pseudo factors s n are modeled by a Dirichlet Process Mixture (DPM) of the Gaussian distributions as

where,  represents the Gaussian distribution with mean µ
l
,
n
and variance
represents the Gaussian distribution with mean µ
l
,
n
and variance  , DP denotes the Dirichlet process, and NIG is short for the conjugate Normal-Inverse-Gamma (NIG) distribution. This DPM model implies a clustering effect on s
n
such that
, DP denotes the Dirichlet process, and NIG is short for the conjugate Normal-Inverse-Gamma (NIG) distribution. This DPM model implies a clustering effect on s
n
such that

and

where, γ n ∈ ℤ represents the cluster label of the n-th sample and is governed by a discrete GEM distribution [17], which defines the stick breaking process with parameter α; this implies that the elements of s n are correlated. Based on (2) and (3), we have

where,  denotes the rectified Gaussian distribution [19]. Since
denotes the rectified Gaussian distribution [19]. Since  and γ
n
are still defined in (4) by the DP, x
n
is hence modeled by the DPM of the rectified Gaussian distributions and the elements of x
n
are accordingly correlated. In contrast to the conventional mixture model, the DPM model enables the number of clusters to be learnt adaptively from the data instead of being predefined.
and γ
n
are still defined in (4) by the DP, x
n
is hence modeled by the DPM of the rectified Gaussian distributions and the elements of x
n
are accordingly correlated. In contrast to the conventional mixture model, the DPM model enables the number of clusters to be learnt adaptively from the data instead of being predefined.
A- the G × L loading matrix, whose element a g , l represents the regulatory coefficient of the g-th gene by the l-th TF. Since a TF is known to regulate only small set of genes, A should be sparse. In our model, the elements of A are assumed to be independent and with the a priori distribution [16]

where, π g , l is the a priori probability of a g , l to be nonzero. For instance, if a TF regulates a total of 500 genes among the 20000 genes in the human genome, then π g , l is equal to

In most cases, π
g
,
l
are likely to be smaller than 10%. In practice, databases such as TRANSFAC [11] and DBD [22] provide information of experimentally validated or predicted target genes of TFs, and this knowledge can be incorporated in the model by setting, for instance, π
g
,
l
= 0. 9, if TF l is known to regulate gene g; or otherwise π
g
,
l
= 0. 025. The variable  defines how much the target genes are loaded on the corresponding TF and with prior distribution
defines how much the target genes are loaded on the corresponding TF and with prior distribution  .
.
c- a vector of constant, which can be considered as the constant term retained when linearizing the general relationship y n = f(x n ) as y n = Ax n + c. It may also be interpreted as static response of gene transcriptional expressions.
e
n
- the G × 1 white Gaussian noise vector characterized by the covariance matrix  and with prior distribution
and with prior distribution  .
.
The overall graphical model is shown in Fig.1.
Graphical model . The Bayesian graphical model is shown here. y n is the observed mRNA gene microarray data, the prior probability of regulation π g , l is extracted from TRANSFAC database, α n , β n , λ 0, α, αa, β a are the hyperparameters, and the rest variables are unknown and need to be estimated.
Equivalent model for centralized observations
To infer a factor model (1) more efficiently, the observation mean is usually removed at the first stage to eliminate the effect of the constant term c, resulting the equivalent model for centralized observations ŷ
n
, where, ŷ
n
= y
n
– µ
y
and  . Traditionally, since the models typically assume zero mean for the factors, the equivalent model for centralized observations remains the same except that the constant term is eliminated, i.e., if y
n
= Ax
n
+ c + e
n
, then, for the centralized data ŷ
n
,
. Traditionally, since the models typically assume zero mean for the factors, the equivalent model for centralized observations remains the same except that the constant term is eliminated, i.e., if y
n
= Ax
n
+ c + e
n
, then, for the centralized data ŷ
n
,

and µ y can be viewed as an ML estimator of the constant term c [23]. For BNFM, however, since the factor mean is no longer zero, the equivalent model for BNFM no longer remains the same as above mentioned traditional model, but instead,

where,


Given sufficient number of samples, the sample mean µ x = [µ x 1, µ x 2, …,µ x L]⊺ can be approximated with the mean of prior distribution (4)(5), which can be calculated numerically. We can also see that the corresponding centralized factors are a shifted version of the original factors, and different samples shift the same amount, so sample clustering effect is still retained. On the other hand, the removed term from data centralization is no longer an estimator of the constant term c, but,

The goal is to obtain the posterior distributions and hence the estimates of A, x n ∀n, γ n ∀n, given y n ∀n and π g , l ∀g, l, which is the TF binding prior information extracted from existing database. For convenience, we let Θ denote all the known and unknown variables.
Gibbs sampling solution
The proposed BNFM model is high dimensional and analytically intractable, so a Gibbs sampling solution is proposed. Gibbs sampling devises a Markov Chain Monte Carlo scheme to generate random samples of the unknowns from the desired but intractable posterior distributions and then approximate the (marginal) posterior distributions with these samples. The key of Gibbs sampling is to derive the conditional posterior distributions and then draw samples from them iteratively until convergence is reached. The proposed Gibbs sampler can be summarized as follows:
Gibbs sampling for BNFA
Iterate the following steps and for the t-th iteration:
-
1.
Sample
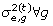 from
from  ;
; -
2.
Sample
 from
from  ;
; -
3.
Sample
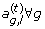 from p(a
g
,
l
|Θ
–a
g,l
);
from p(a
g
,
l
|Θ
–a
g,l
); -
4.
for n = 1 to N
Sample  from
from  ;
;
Sample  from
from  ;
;
Sample  from p(s
n
|Θ
–s
n
);
from p(s
n
|Θ
–s
n
);
Note that  are marginalized and therefore does not need to be sampled. The algorithm iterates until the convergence of samples, which can be assessed by the scheme described in [24], [chap. 11.6]. The samples after convergence will be collected to approximate the marginal posterior distributions and the estimates of the unknowns. Since µ
x
can be approximated and calculated numerically, the factor x
n
can be recovered from the centralized factor
are marginalized and therefore does not need to be sampled. The algorithm iterates until the convergence of samples, which can be assessed by the scheme described in [24], [chap. 11.6]. The samples after convergence will be collected to approximate the marginal posterior distributions and the estimates of the unknowns. Since µ
x
can be approximated and calculated numerically, the factor x
n
can be recovered from the centralized factor  with (9). The required conditional distributions of the above proposed Gibbs sampling solution are detailed in the next.
with (9). The required conditional distributions of the above proposed Gibbs sampling solution are detailed in the next.
Conditional distributions of the proposed Gibbs sampling solution
For simplicity, we let x n and y n denote the centralized factors and data in this section.

Let E = Y – AX and e g = [e g ,1, ⋯, e g , N ]T, then,

where, ŷ g , l = x l a g , l + e g , x l = [x l ,1,⋯, x l , n ]T and e g = [e g ,1, ⋯, e g , N ]T . The posterior distribution of a g , l ,

where Z
0 is a normalizing constant,  is the posterior probability of a
g
,
l
≠ 0 and BF
01 is the Bayes factor of model a
g
,
l
= 0 versus model a
g
,
l
≠ 0
is the posterior probability of a
g
,
l
≠ 0 and BF
01 is the Bayes factor of model a
g
,
l
= 0 versus model a
g
,
l
≠ 0

with  is the posterior distribution for a
g
,
l
≠ 0 and defined by
is the posterior distribution for a
g
,
l
≠ 0 and defined by

where,  and
and  , and π
g
,
l
is the prior knowledge of the probability of a
g
,
l
to be non-zero. When π
g
,
l
= 0. 5, i.e, a noninformative prior on sparsity is assumed,
, and π
g
,
l
is the prior knowledge of the probability of a
g
,
l
to be non-zero. When π
g
,
l
= 0. 5, i.e, a noninformative prior on sparsity is assumed,  depends only on BF
01, and
depends only on BF
01, and  when BF
01 > 1. Since model selection based BF
01 favors a
g
,
l
= 0, it suggests that this Bayesian solution favors sparse model even when π
g
,
l
= 0. 5.
when BF
01 > 1. Since model selection based BF
01 favors a
g
,
l
= 0, it suggests that this Bayesian solution favors sparse model even when π
g
,
l
= 0. 5.

It should be noted that γ
n
does not depend on x
n
in the distribution. It is intended that samples of γ
n
from this distribution are not affected by the immediate sample of x
n
, thus achieving faster convergence of the sample Markov chains. To derive this distribution, first let ŷ
l
,
n
= a
l
x
l
,
n
+ e
n
with a
l
being the l-th column of A and hence  . Then,
. Then,

where  denotes a new cluster other than the existing
denotes a new cluster other than the existing  represents the set of the pseudo factors besides s
l
that also belong to cluster k, N
–l,k
is size of
represents the set of the pseudo factors besides s
l
that also belong to cluster k, N
–l,k
is size of  , and
, and

with,

where,

and,

Noted that, for a new cluster,  and N
–l
,
k
= 0, and
and N
–l
,
k
= 0, and  can be derived from g
k
for
can be derived from g
k
for  similarly.
similarly.

This distribution can be expressed as

where,  represents the truncated Gaussian with parameters
represents the truncated Gaussian with parameters  and between the interval (–µ
x
,+∞), and,
and between the interval (–µ
x
,+∞), and,


According to the graphical model, given x l ,n, the conditional distribution of s l , n does not depend on y 1:N ; As the predictive density p(s l , n |s – l , n , γ l ) is shown to be a Student-t distribution, which can be conveniently approximated as a normal distribution when N –l , k is large:

and conditional distribution can be expressed as

where, π s l,n = 1 – sgn (x l , n + µ x )

Let the residuals E = Y – AX, and we have,  , where e
g
= [e
g
,1, e
g
,2, …, e
g
,
N
]⊺ Given the conjugate Inverse-Gamma prior, we have
, where e
g
= [e
g
,1, e
g
,2, …, e
g
,
N
]⊺ Given the conjugate Inverse-Gamma prior, we have

where Inv-Gamma represents the Inverse-Gamma distribution and


With the prior distribution  , the conditional probability of
, the conditional probability of  is,
is,

where,  and
and  , and N
a
,
l
is the size of
, and N
a
,
l
is the size of  .
.
Results
Test on simulated system
The proposed BNFM model was first tested on a simulated system, in which the microarray data consists of the expression profiles of 150 genes with 40 samples. The samples form 5 clusters and the 150 genes were assumed to be regulated by 10 TFs. The sparsity of loading matrix was set at 10%, which means that on average each gene is regulated by 1 TFs, and each TF regulates 15 genes. To simulate a practical imperfect database, the precision and recall of the prior knowledge were both set equal to 0.9 each, i,e., 90% of the database recorded regulations indeed happened in this specific data set (10% of the database recorded regulations may be context-specific and didn’t happen in the data); and 90% of the true regulations was recorded in the database (10% of true regulations are not in the database). This setting indicates that the recorded prior regulations may not exist in the experiment, and the unknown regulations could exist. Since this is a relatively large data set involving sampling of many variables, instead of examining convergence based on [24], [chap. 11.6], we adopted a more practical strategy by running a single MCMC chain for 10000 iterations with a burn-in period of 2000 iterations [25].
Since the algorithm estimates the loading matrix, the factors, the clustering result, and TF regulatory targets, to evaluate the performance, four respective metrics were computed. Particularly, in order to systematically evaluate the clustering result, a Van Rijsbergen’s F metric [26] that combines the BCubed precision and recall [27] was implemented as suggested in [28]. More specifically, let L(e) and C(e) be the category and the cluster of an item e. Then, the correctness of the relation between e and e′ is defined by

That is, two items are correctly related when they share the same cluster. Moreover, the BCubed precision and recall are formally defined as

These two metrics can be further combined using Van Rijsbergen’s F metrics:

The F metrics satisfy all the 4 formal constraints defined in [28] including cluster homogeneity, cluster completeness, rag bag, and cluster size vs. quantity. We adopt the F metrics to evaluate the clustering result in the following tests. Similarly, a Van Rijsbergen’s F metric that combines the target prediction precision and recall is used to measure the target prediction result. Since our model can avoid sign ambiguity problem, the loading and factor estimations were evaluated using its Pearson’s correlation with their true values.
Experiments were carried out to test the impact of noise (Fig. 2), database precision (Fig. 3) and database recall (Fig. 4) on the performance of the algorithm. It can be seen from the simulation result that, at the low noise level or with high quality prior database, the developed algorithm can produce satisfactory result. Expectedly, the performance of the algorithm decreases as the noise variance increases or database quality decreases. However, the clustering performance is more sensitive to noise (Fig.2), while target prediction result relies more heavily on the quality of database prior knowledge (Fig. 3-4), because database directly support regulation posterior probability through its prior probability. In summary, the simulation results are indicative of satisfactory performance of the developed Gibbs sampling algorithm.
Impact of noise. The performance vs noise is shown here. Two noise conditions  are tested. It can be seen from the figure that, the algorithm performance deceases as noise increases. While the clustering result relies on noise heavily (Fig.2-a), the target prediction is relatively more robust against noise (Fig.2-c).
are tested. It can be seen from the figure that, the algorithm performance deceases as noise increases. While the clustering result relies on noise heavily (Fig.2-a), the target prediction is relatively more robust against noise (Fig.2-c).
Impact of database precision. The performance vs database precision is shown here. It can be seen from the figure that, the algorithm performance deceases as noise increases. While the target prediction relies on the quality of database heavily (Fig.3-c), the clustering result is relatively robust against database quality (Fig.3-a) .
Impact of database recall. The performance vs database recall is shown here. It can be seen from the figure that, the algorithm performance deceases as noise increases. While the target prediction relies on the quality of database heavily (Fig.4-c), the clustering result is relatively robust against database quality (Fig.4-a) .
Test on breast cancer data
After validating the performance of the proposed algorithm by simulation, the algorithm was then applied to the breast cancer microarray data published in [29–32]. Particularly, we applied the algorithm to 53 samples of grade 3 ER+ breast cancer. All samples came with gene microarray expression, ER status and survival time information. For the settings of the algorithm, we first manually selected a total of 15 TFs that are reported to be relevant to breast cancer (Table 1) and then retrieved a total of 199 regulated target genes (Table 2) by these TFs from TRANSFAC database [11] (Release 2009.4). We assume that TRANSFAC record has a 90% precision and 90% recall, suggesting that the known regulations may be context-specific and unknown regulations could exist. From the precision and the recall, the prior probability of the loading matrix can be determined. Based on these settings, the proposed approach was applied to the breast cancer data set to infer the underlying regulatory networks and TF activities. The posterior distribution of the loading matrix (Fig.5) gives insight into the sparsity of inferred TF mediated regulation. It can be seen that the posterior probability of regulations fall into 2 distinct groups, i.e., one group has very small posterior probabilities, which correspond to regulations that do not exist; while the other group have larger posterior probabilities, which correspond the regulations that are likely to exist. Fig. 6 depicts possible regulations and their posterior probabilities (rounded by 0.1) in a network, demonstrating the capability of the proposed approaches to identify possible TF regulated target genes.
Network of the posterior probability of regulations . The network depicts possible regulations and their posterior probabilities (rounded by 0.1), where a edge indicates a possible regulation from a TF to a gene, and the line width of the edge represents the probability of the particular regulation exists, with thicker line width stands for larger probability; and vise versa.
When setting the cut-off threshold 0.5, the result confirmed 281 regulations among the 282 regulations that were defined in the TRANSFAC database, and identified 25 new regulations that are not recorded in the database. This fact demonstrates the ability of our algorithm to discover new regulations and discern context-dependent regulations among the prior knowledge, and the reconstructed network is shown in Fig. 7, showing the capability of the proposed approach to identify both the strength (represented by edge width) and the type (represented by edge color) of transcriptional regulations.
Network of the regulation coefficients. The network shows regulation coefficients, where an edge between a TF and a gene indicates the gene is regulated by the TF, and the color of the edge indicates the regulation types (red for up-regulation, and blue for down regulations), and the line width stands for the regulation strength.
Along with the estimates of regulatory coefficients, the transcription factor activities and the sample cluster attributes were also obtained. Fig.8 depicts the estimated TF activities, with the patient samples grouped according to the clustering result, and it clearly shows the coordinated clustering effects. To further gain insights into the clinical outcomes of different patient groups defined by the TF activities, survival analysis was carried out and it confirmed the survival difference between the the 1st and 2nd clusters (p = 0. 05) as shown in Fig.9. Previous studies based on expression levels [33–36] identified 5 major subtypes (luminal A, luminal B, basal, ERBB2 overexpressing, and normal-like). We compared the pair-wise survival difference between our clustering (3 clusters) and previous result (5 clusters). It shows the superior performance of our method (Table 3) over the previous computation based method (Table 4).
Estimated transcription factor expression. The tested samples fall into 3 major clusters with 24, 11 and 11 samples. The rest 7 samples may be considered as outliers that are not classified. In accordance with the sample clustering result, the recovered TF shows 3 major clustering patterns with a few outliers.
Discussion
We proposed a new approach to uncover the transcriptional regulatory networks from microarray gene expression profiles. We discuss next a few distinct features of it.
First, to reflect the fact that a TF only regulates a small number of genes among the whole genome, the loading matrix of the factor model is constrained by a sparse prior [16], which directly reflects our existing knowledge of the particular TF-gene regulation, i.e., if the regulation exists according to prior knowledge, the probability of the corresponding component of the loading matrix to be non-zero is large; or otherwise, very small. The introduction of sparsity significantly constrains the factor model and helps to enable the inference of a set of correlated samples.
Second, since the activities of TFs cannot be negative, the factors are modeled by a non-negative rectified Gaussian distribution [19], which not only is consistent with the physical fact of TF regulation but also avoids the inherent sign ambiguity problem of the factor models. Noted that, a rectified Gaussian distribution  is different from a truncated Gaussian
is different from a truncated Gaussian  in that:
in that:

indicating that the rectified Gaussian model can also describe the possible suppressed state of TFs, which nevertheless cannot be modeled by the truncated Gaussian distribution. A comparison of Gaussian, rectified Gaussian, and truncated Gaussian is shown as Fig.10. In our model, the non-negativity is constrained only on the factor matrix; the elements of loading matrix can be either positive or negative, which models the corresponding up- or down-regulation of TFs. This is different from non-negative matrix factorization (NMF) [13, 15, 37, 38]. NMF enforces that both the loading matrix and the factor matrix must be non-negative, i.e., all elements must be equal to or greater than zero. With the capability of modeling both the up- or down-regulations, the proposed BNFM is more appropriate for modeling the TF regulation than NMF.
Comparison of original, rectified and truncated Gaussian distributions. The probability distribution function of Gaussian, rectified Gaussian and truncated Gaussian are shown in this figure. The range of Gaussian distribution  is from (–∞, ∞), the range of rectified Gaussian
is from (–∞, ∞), the range of rectified Gaussian  is [0, ∞], and the range of truncated Gaussian
is [0, ∞], and the range of truncated Gaussian  is (0, 3).
is (0, 3).
To model the samples correlation due to, for instance, cancer subtypes, the samples are modeled by a Dirichlet process mixture (DPM), which imposes clustering effect among samples and can automatically determine the optimal number of clusters from data rather than be predefined in the algorithm. Forth, other types of data, such as ChIP-chip data [39–41] and DNA methylation data [42] can be conveniently integrated with gene expression data [43] under the proposed framework by setting a slightly different prior probabilities to the loading matrix. Integrating additional data types can potentially improve the accuracy of the reconstructed networks. [12].
However, the proposed model is not without shortcomings. First, this model can not yet capture regulations from TFs that are not specified in the prior knowledge database. In reality, it is possible that some TFs that are not specified in the prior knowledge actually regulate the gene transcription. Second, the algorithm may not converge in a reasonable number of iterations on a large data set, thus cannot yet be applied to genome wide data set. Because the model parameters are high dimensional and highly correlated, the speed of convergence may significantly slow down on a large data set [44, 45]. However, such restriction on the size of genes and TFs forces us to focus the analysis on most relevant genes and TFs, making the analysis more targeted and easy to interpret. We demonstrate in section Result, how such analysis can be carried out starting from a whole genome microarray data. With the advancement in ChIP-seq technology and increasing knowledge of TFs biological functions, the proposed model could be applied for a genome-wide study in the future.
Thirdly, the prior knowledge may still need to be properly evaluated. If the prior knowledge is considered an estimation of the true TRN, when the precision p, recall r of prior information and the sparsity of the loading matrix s is given, the prior probability of the g-th gene to be a target of the l-th TF π g , l can be calculated as follows:

However, the precision or recall of the prior knowledge database are only arbitrarily specified (both 90%). In practice, the quality of prior knowledge should be evaluated first before more reasonable prior probabilities of regulations can be assigned.
Conclusions
A Bayesian factor model that has sparse loading matrix, non-negative factors, and correlated samples, was proposed to unveil the latent activities of transcription factors and their targeted genes from observed gene mRNA expression profiles. By naturally incorporating the prior knowledge of TF regulated genes, the sparsity constraint of the loading matrix, the non-negativity constraints of TF activities, the regulation coefficients and TF activities can be estimated. A Gibbs sampling solution was proposed and model inference. The effectiveness and validity of the model and the proposed Gibbs sampler were evaluated on simulated systems. The proposed method was applied to the breast cancer microarray data and a TF regulated network for breast cancer data was reconstructed. The inferred TF activities indicates 3 patients clusters, two of which possess significant differences in survival time after treatment. These results demonstrated that the BNFM provides a viable approach to reconstruct TF mediated regulatory networks and estimate TF activities from mRNA expression profiles. The BNFM will be an important tool for not only understanding the transcriptional regulation but also predicting the clinical outcomes of treatment.
References
Hobert O: Gene regulation by transcription factors and microRNAs. Science 2008,319(5871):1785. 10.1126/science.1151651
Huang Y, Tienda-Luna I, Wang Y: Reverse engineering gene regulatory networks. Signal Processing Magazine, IEEE 2009, 26: 76–97.
Greenbaum D, Colangelo C, Williams K, Gerstein M: Comparing protein abundance and mRNA expression levels on a genomic scale. Genome Biol 2003,4(9):117. 10.1186/gb-2003-4-9-117
Gygi S, Rochon Y, Franza B, Aebersold R: Correlation between protein and mRNA abundance in yeast. Molecular and Cellular Biology 1999,19(3):1720.
Sabatti C, James G: Bayesian sparse hidden components analysis for transcription regulation networks. Bioinformatics 2006,22(6):739. 10.1093/bioinformatics/btk017
Sanguinetti G, Lawrence N, Rattray M: Probabilistic inference of transcription factor concentrations and gene-specific regulatory activities. Bioinformatics 2006,22(22):2775. 10.1093/bioinformatics/btl473
Yu T, Li K: Inference of transcriptional regulatory network by two-stage constrained space factor analysis. Bioinformatics 2005,21(21):4033. 10.1093/bioinformatics/bti656
Boulesteix A, Strimmer K: Predicting transcription factor activities from combined analysis of microarray and ChIP data: a partial least squares approach. Theoretical Biology and Medical Modelling 2005, 2: 23. 10.1186/1742-4682-2-23
Kao K, Yang Y, Boscolo R, Sabatti C, Roychowdhury V, Liao J: Transcriptome-based determination of multiple transcription regulator activities in Escherichia coli by using network component analysis. Proceedings of the National Academy of Sciences 2004,101(2):641. 10.1073/pnas.0305287101
Meng J, Zhang JM, Qi YA, Chen Y, Huang Y: Uncovering Transcriptional Regulatory Networks by Sparse Bayesian Factor Model. Eurasip Journal On Advances In Signal Processing 2010.
Matys V, Fricke E, Geffers R, Gossling E, Haubrock M, Hehl R, Hornischer K, Karas D, Kel A, Kel-Margoulis O, et al.: TRANSFAC (R): transcriptional regulation, from patterns to profiles. Nucleic acids research 2003, 31: 374. 10.1093/nar/gkg108
Ideker Trey, JHL Dutkowski: Boosting Signal-to-Noise in Complex Biology: Prior Knowledge Is Power. Cell 2011,144(6):860–863. 10.1016/j.cell.2011.03.007
Qi Q, Zhao Y, Li M, Simon R: Non-negative matrix factorization of gene expression profiles: a plug-in for BRB-ArrayTools. Bioinformatics 2009,25(4):545. 10.1093/bioinformatics/btp009
Hoyer P: Non-negative matrix factorization with sparseness constraints. The Journal of Machine Learning Research 2004, 5: 1469.
Brunet J, Tamayo P, Golub T, Mesirov J: Metagenes and molecular pattern discovery using matrix factorization. Proceedings of the National Academy of Sciences of the United States of America 2004,101(12):4164. 10.1073/pnas.0308531101
Carvalho C, Chang J, Lucas J, Nevins J, Wang Q, West M: High-dimensional sparse factor modeling: Applications in gene expression genomics. Journal of the American Statistical Association 2008,103(484):1438–1456. 10.1198/016214508000000869
Sudderth E: Graphical models for visual object recognition and tracking. PhD thesis. Massachusetts Institute of Technology; 2006.
Ferguson T: A Bayesian analysis of some nonparametric problems. The annals of statistics 1973,1(2):209–230. 10.1214/aos/1176342360
Socci N, Lee D, Sebastian Seung H: The rectified Gaussian distribution. Advances in Neural Information Processing Systems 1998, 350–356.
Cui X, Churchill G: Statistical tests for differential expression in cDNA microarray experiments. Genome Biol 2003,4(4):210. 10.1186/gb-2003-4-4-210
Wong C: Differential Expression and Annotation. 2009.
Wilson D, Charoensawan V, Kummerfeld S, Teichmann S: DBD-taxonomically broad transcription factor predictions: new content and functionality. Nucleic Acids Research 2008,36(Database issue):D88.
Tipping M, Bishop C: Probabilistic principal component analysis. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1999,61(3):611–622. 10.1111/1467-9868.00196
Gelman A, Carlin J, Stern H, Rubin D: Bayesian data analysis. London, Glasgow, et al 1995.
Thompson W, Newberg L, Conlan S, McCue L, Lawrence C: The Gibbs centroid sampler. Nucleic Acids Research 2007.
Van Rijsbergen C: Foundation of evaluation. Journal of Documentation 1974,30(4):365–373. 10.1108/eb026584
Bagga A, Baldwin B: Entity-based cross-document coreferencing using the vector space model. In Proceedings of the 17th international conference on Computational linguistics-Volume 1. Association for Computational Linguistics Morristown, NJ, USA; 1998:79–85.
Amigó E, Gonzalo J, Artiles J, Verdejo F: A comparison of extrinsic clustering evaluation metrics based on formal constraints. Information Retrieval 2009,12(4):461–486. 10.1007/s10791-008-9066-8
Hoadley K, Weigman V, Fan C, Sawyer L, He X, Troester M, Sartor C, Rieger-House T, Bernard P, Carey L, et al.: EGFR associated expression profiles vary with breast tumor subtype. BMC genomics 2007, 8: 258. 10.1186/1471-2164-8-258
Mullins M, Perreard L, Quackenbush J, Gauthier N, Bayer S, Ellis M, Parker J, Perou C, Szabo A, Bernard P: Agreement in breast cancer classification between microarray and quantitative reverse transcription PCR from fresh-frozen and formalin-fixed, paraffin-embedded tissues. Clinical chemistry 2007,53(7):1273. 10.1373/clinchem.2006.083725
Herschkowitz J, Simin K, Weigman V, Mikaelian I, Usary J, Hu Z, Rasmussen K, Jones L, Assefnia S, Chandrasekharan S, et al.: Identification of conserved gene expression features between murine mammary carcinoma models and human breast tumors. Genome biology 2007,8(5):R76. 10.1186/gb-2007-8-5-r76
Herschkowitz J, He X, Fan C, Perou C: The functional loss of the retinoblastoma tumour suppressor is a common event in basal-like and luminal B breast carcinomas. Breast Cancer Res 2008,10(5):R75. 10.1186/bcr2142
Perou C, Sørlie T, Eisen M, van de Rijn M, Jeffrey S, Rees C, Pollack J, Ross D, Johnsen H, Akslen L, et al.: Molecular portraits of human breast tumours. Nature 2000,406(6797):747–752. 10.1038/35021093
Sørlie T, Perou C, Tibshirani R, Aas T, Geisler S, Johnsen H, Hastie T, Eisen M, Van De Rijn M, Jeffrey S, et al.: Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications. Proceedings of the National Academy of Sciences of the United States of America 2001,98(19):10869. 10.1073/pnas.191367098
Sørlie T, Tibshirani R, Parker J, Hastie T, Marron J, Nobel A, Deng S, Johnsen H, Pesich R, Geisler S, et al.: Repeated observation of breast tumor subtypes in independent gene expression data sets. Proceedings of the National Academy of Sciences of the United States of America 2003,100(14):8418. 10.1073/pnas.0932692100
Shai R, Shi T, Kremen T, Horvath S, Liau L, Cloughesy T, Mischel P, Nelson S: Gene expression profiling identifies molecular subtypes of gliomas. Oncogene 2003,22(31):4918–4923. 10.1038/sj.onc.1206753
Kim P, Tidor B: Subsystem identification through dimensionality reduction of large-scale gene expression data. Genome Research 2003,13(7):1706. 10.1101/gr.903503
Li T, Ding C: The relationships among various nonnegative matrix factorization methods for clustering. Data Mining, 2006.ICDM’06. Sixth International Conference on 2006, 362–371.
Lieb J, Liu X, Botstein D, Brown P: Promoter-specific binding of Rap1 revealed by genome-wide maps of protein-DNA association. Nature genetics 2001,28(4):327–334. 10.1038/ng569
Iyer V, Horak C, Scafe C, Botstein D, Snyder M, Brown P: Genomic binding sites of the yeast cell-cycle transcription factors SBF and MBF. Nature 2001,409(6819):533–538. 10.1038/35054095
Ren B, Robert F, Wyrick J, Aparicio O, Jennings E, Simon I, Zeitlinger J, Schreiber J, Hannett N, Kanin E, et al.: Genome-wide location and function of DNA binding proteins. Science’s STKE 2000,290(5500):2306.
Jaenisch R, Bird A: Epigenetic regulation of gene expression: how the genome integrates intrinsic and environmental signals. Nature genetics 2003, 33: 245–254. 10.1038/ng1089
Tasheva E, Klocke B, Conrad G: Analysis of transcriptional regulation of the small leucine rich proteoglycans. Mol Vis 2004, 10: 758–772.
Justel A: Gibbs sampling will fail in outlier problems with strong masking. Journal of Computational and Graphical Statistics 1996,5(2):176–189. 10.2307/1390779
Borgs C, Chayes J, Frieze A, Kim J, Tetali P, Vigoda E, Vu V: Torpid mixing of some Monte Carlo Markov chain algorithms in statistical physics. ANNUAL SYMPOSIUM ON FOUNDATIONS OF COMPUTER SCIENCE, Volume 40 1999, 218–229.
Acknowledgements
This article has been published as part of Proteome Science Volume 9 Supplement 1, 2011: Proceedings of the International Workshop on Computational Proteomics. The full contents of the supplement are available online at http://www.proteomesci.com/supplements/9/S1.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Meng, J., Zhang, J.(., Chen, Y. et al. Bayesian non-negative factor analysis for reconstructing transcription factor mediated regulatory networks. Proteome Sci 9 (Suppl 1), S9 (2011). https://doi.org/10.1186/1477-5956-9-S1-S9
Published:
DOI: https://doi.org/10.1186/1477-5956-9-S1-S9


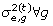 from
from  ;
; from
from  ;
;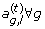 from p(a
g
,
l
|Θ
–a
g,l
);
from p(a
g
,
l
|Θ
–a
g,l
);







